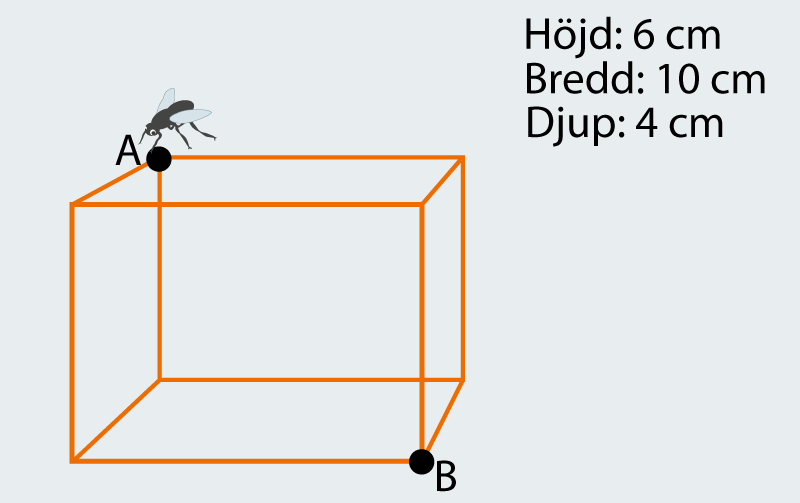
I de här tre problemen skall du avgöra hur lång den kortaste vägen är för myran eller flugan från punkt A till punkt B.
Viktigt! I alla figurer hittar du ett litet djur och ett rätblock. Rätblocket är ihåligt där kanterna går att gå på. Däremot kan myran inte gå på sidorna.
I de här problemen kan det vara bra att du känner till pythagoras sats.
Kortaste vägen 1
Hur lång väg är den kortaste vägen för myran från punkt A till punkt B?
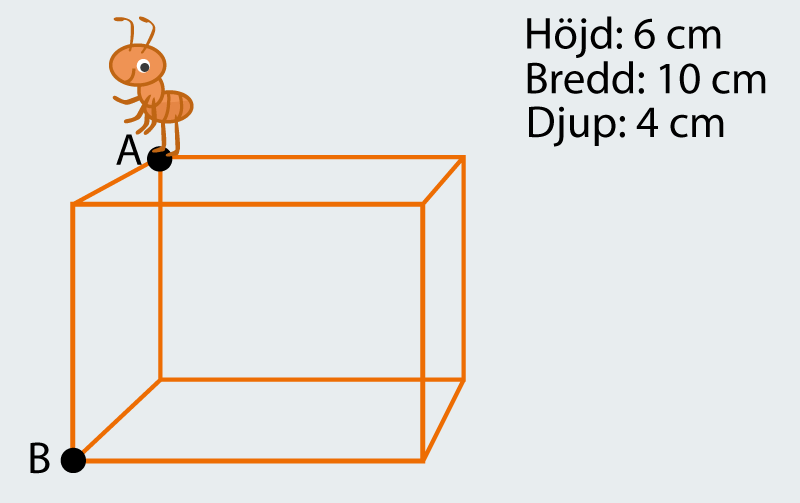
Kortaste vägen 2
Hur lång väg är den kortaste vägen för myran från punkt A till punkt B?
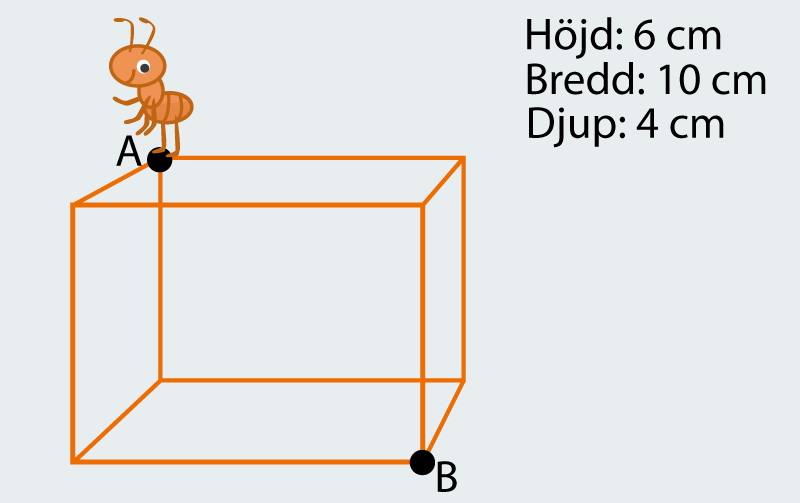
Kortaste vägen 3
Hur lång väg är den kortaste vägen för flugan från punkt A till punkt B?